Viscoelastic Bodies

OpenSWPC adopts the generalized Zener body (GZB) as a model of the viscoelastic body. It consists of several viscoelastic Zener bodies with different relaxation times to attain nearly constant Q in a wide frequency range. As a consequence, it accompanies the frequency-dependent body wavespeed via physical dispersion (e.g., Aki and Richards, 2002¹); therefore, users should specify the reference frequency in which the velocity model is given.

Figure

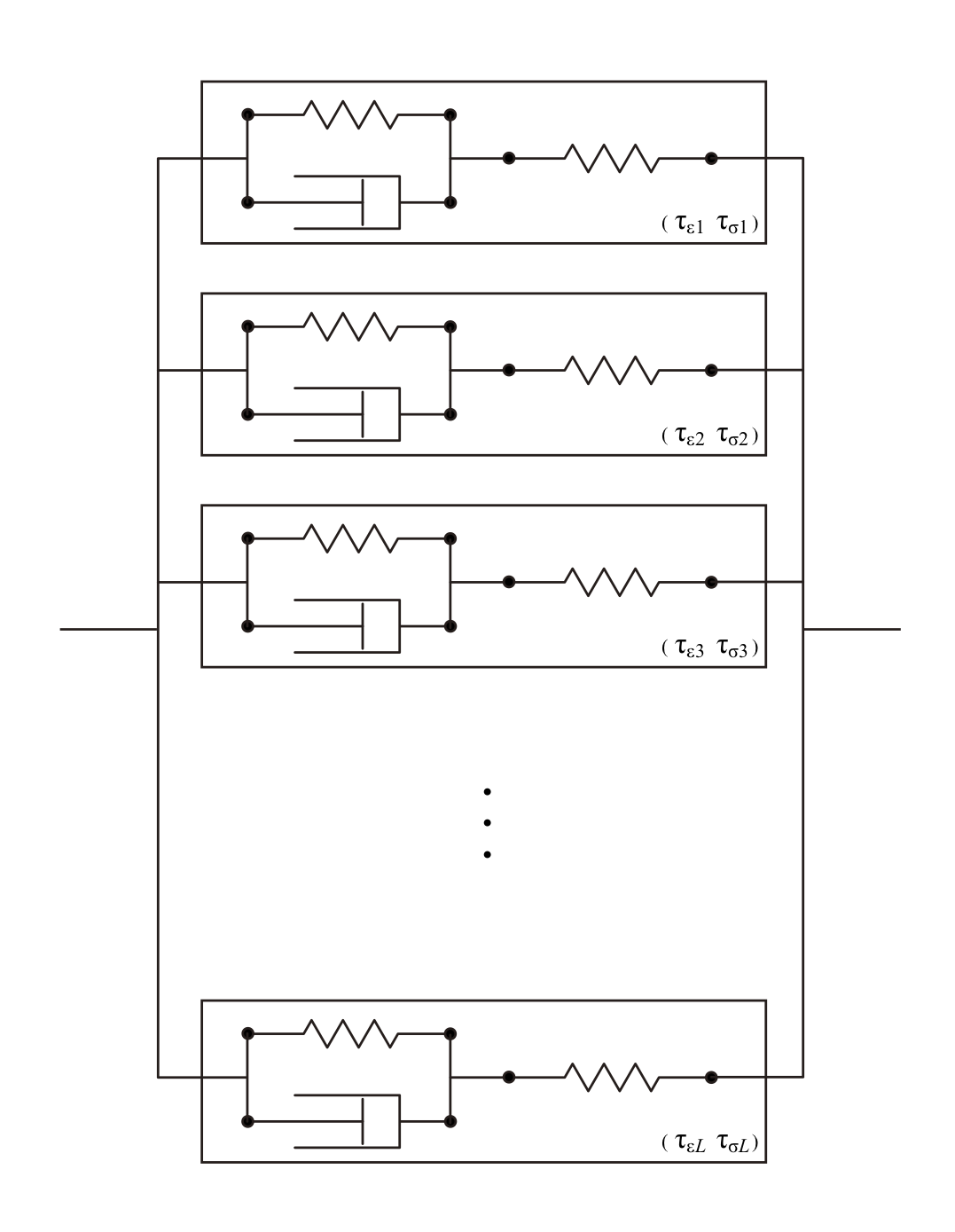
A schematic illustration of the Generalized Zener body. Zener Body (boxes) having different chracteristic times are connnected.

Figure

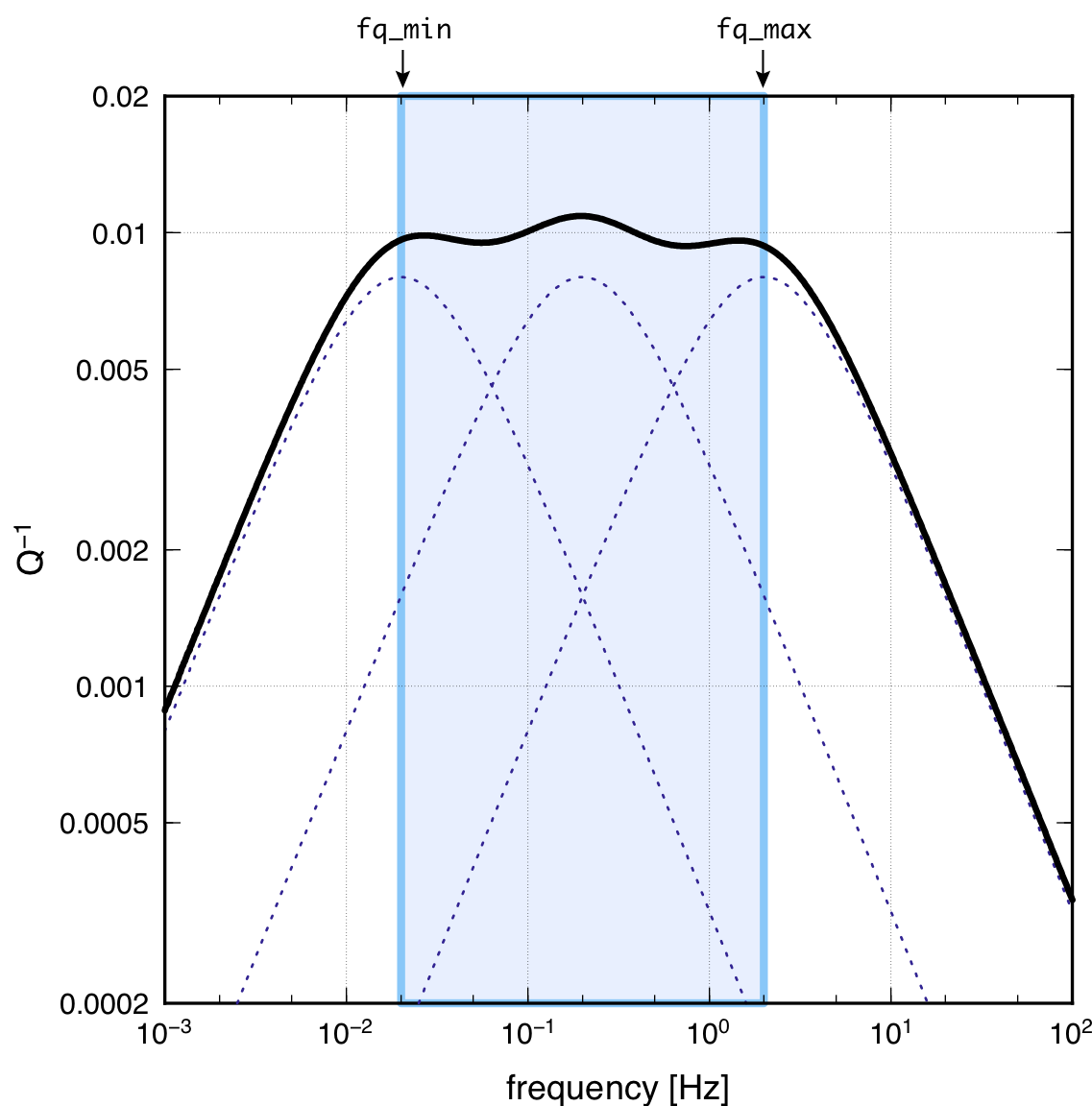
Example of frequency dependence of the intrinsic attenuation $Q^{-1}$ for a GZB of NM=3. The thick solid line shows the attenuation of the entire model, while the dotted lines show the attenuation model for each constituent of the Zener body. The vertical lines show the specified minimum and maximum frequencies for the constant $Q$ range.

GZB consists of $N_M$ Zener bodies, as schematically shown in the Figure above. This viscoelastic body is described by the relaxation functions for an elastic moduli $\pi \equiv \lambda + \mu$ and $\mu$, as

$$\begin{align} \begin{split} \psi_\pi \left( t \right) &= \pi_R \left( 1 - \frac{1}{N_M} \sum_{m=1}^{N_M} \left( 1 -\frac{ \tau_m^{\epsilon P}}{\tau_{m}^\sigma} \right) e^{-t/\tau^\sigma_m} \right) H(t) \\ \psi_\mu \left( t \right) &= \mu_R \left( 1 - \frac{1}{N_M} \sum_{m=1}^{N_M} \left( 1 -\frac{ \tau_m^{\epsilon S}}{\tau^\sigma_m} \right) e^{-t/\tau^\sigma_m} \right) H(t) \end{split} \end{align}$$

where $\tau_m^\sigma$ is the relaxation time of the $m$-th body, $\pi_R\equiv \lambda_R + 2 \mu_R$ and $\mu_R$ are the relaxed moduli, and $\tau_m^{\varepsilon P}$ and $\tau_m^{\varepsilon S}$ are creep times of the P- and S-waves, respectively. The wide frequency range of constant $Q$ is achieved by connecting Zener bodies with different relaxation times. In addition, the intrinsic attenuations of the P- and S-waves ($Q_P$ and $Q_S$, respectively) can be defined independently by choosing different creep times between the elastic moduli $\pi$ and $\mu$.

$$\begin{align} \begin{split} &\dot \sigma_{ii} (t) = \left( \dot \psi_\pi (t) - 2 \dot \psi_\mu (t) \right) \ast \partial_k v_k(t) + 2 \dot \psi_\mu(t) \ast \partial_i v_i(t) \\ &\dot\sigma_{ij} (t) = \dot \psi_\mu(t) \ast \left( \partial_i v_j(t) + \partial_j v_i(t) \right) \end{split} \end{align}$$

The convolution appearing in the constitutive equation can be avoided by defining the memory variables (Robertsson, 1994²) and solving the auxiliary differential equations for them. We also adopt the $\tau$-method of Blanch (1994³) to automatically choose the creep times that achieve a constant $Q$ condition.

Parameters

**fq_min **

Minimum frequency of the constant-$Q$ model.

**fq_max **

Maximum frequency of the constant-$Q$ model.

**fq_ref **

Reference frequency at which the velocity model is given.

The $Q^{-1}$ value becomes nearly constant between the frequencies of fq_min and fq_max. Outside of the band, the attenuation becomes weaker with increasing/decreasing frequency. As shown in this figure, the nearly constant $Q^{-1}$ is achieved using three different viscoelastic bodies. If one needs to make $Q^{-1}$ constant over a wider frequency range, the hard-coded parameter NM should be increased. However, this leads to a significant increase in the memory usage and computational loads. The frequency dependence of $Q^{-1}$ with the parameters specified above can be investigated using the program qmodel_tau.x.

Note that velocities of P and S waves depends on a frequency if one use constant-$Q$ model at a wide frequency band. A parameter fq_ref is used as a reference frequency at which the input velocities are defined.

---

1. Aki, K., & Richards, P. G. (2002), Quantitative Seismology, 2nd Edition, University Science Books. ↩

2. Robertsson, J. O., J. O. Blanch, and W. W. Symes (1994), Viscoelastic finite-difference modeling, Geophysics, 59(9), 1444–1456, doi:10.1190/1.1443701. ↩

3. Blanch, J. O., J. O. Robertsson, and W. W. Symes (1994), Modeling of a constant Q: methodology and algorithm for an efficient and optimally inexpensive viscoelastic technique, Geophysics, 60, 176–184, doi:10.1111/j.1365-246X.2004.02300.x. ↩